[Python] 이분매칭 알고리즘 baseline

이분매칭 알고리즘이란?

2개의 정점 그룹이 있을 때, 그룹에서 그룹으로 정점의 최대 매칭을 찾는 알고리즘입니다.

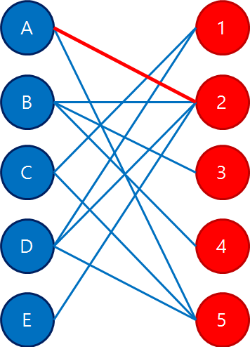
아래와 같은 두 그룹의 정점이 있다고 합시다.

각 그룹을 연결할 수 있는 간선의 정보입니다.
A: 2, 5
B: 2, 3, 4
C: 1, 5
D: 1, 2, 5
E: 2

 

위 간선들 중에서 정점을 한 번만 사용해서 최대 매칭을 이룰 수 있게 만드는 것이 이분매칭 알고리즘의 목적입니다.

알고리즘은 깊이 우선 탐색(DFS)로 진행이 되며, 과정은 아래와 같습니다.

 

우선 A와 매칭이 가능한 1을 매칭 시킵니다.

현재 연결 정보
A -- 2
B -- 
C -- 
D -- 
E -- 

A는 매칭했으니 B를 보도록 합시다.

B를 2와 매칭시키려했는데 이미 A가 차지했네요. 이런 경우는 이전에 매칭됐던 A가 양보를 해줍니다.

따라서 A는 5와 매칭이 되고, B는 2와 매칭할 수 있게 됩니다.

현재 연결 정보
A -- 5
B -- 2
C -- 
D -- 
E -- 

 

이제 C를 봅시다.

 

C는 1과 5로 매칭이 가능한 정점입니다. 아무도 매칭이 안된 정점 1과 매칭이 순조롭게 이뤄졌네요.

현재 연결 정보
A -- 5
B -- 2
C -- 1
D -- 
E -- 

 

이제 D를 봅시다.

D는 정점 1, 2, 5와 매칭이 가능합니다.

D와 연결해야하는 정점 1이 C와 매칭이 되어있네요. C한테 양보하라 합시다.

C는 어쩔 수 없이 정점 5와 매칭해야하는 상황입니다. 그런데 정점 5는 이미 A와 매칭이 되어있네요.

A는 어쩔 수 없이 정점 2와 매칭해야하는 상황입니다. 그런데 정점 2도 이미 B와 매칭이 되어있네요.

B는 어쩔 수 없이 정점 3과 매칭해야하는 상황입니다. 다행히 정점 3과 매칭할 수 있네요.

 

조금 복잡해졌는데 할만 한 것 같습니다.

현재 연결 정보
A -- 2
B -- 3
C -- 5
D -- 1
E -- 

 

이제 E를 보면 됩니다.

그러나 E는 매칭할 수 있는 방법이 없습니다.

따라서 최대 매칭 수는 4가 됩니다.

---

Baseline Code

def bimatch(N):                                           
    if visited[N]:                                        
        return False                                      
    visited[N] = True                                     
                                                          
    for num in graph[N]:             
        # 매칭이 안된 정점이거나, 이미 매칭된 정점이 다른 매칭으로 바꿀 수 있다면            
        if selected[num] == -1 or bimatch(selected[num]):         
            selected[num] = N                                
            return True                                   
                                                          
    return False          

if __name__ == '__main__':
    # 왼쪽 정점수, 오른쪽 정점 수
    n, m = 5, 5

    # 왼쪽 정점에서 연결 가능한 오른쪽 정점 번호들
    graph = [[2, 5], [2, 3, 4], [1, 5], [1, 2, 5], [2]]

    # 오른쪽 그룹과 매칭된 왼쪽 그룹 정점 번호
    selected = [-1] * (m + 1)

    for i in range(n):            
        visited = [False] * (n)      
        bimatch(i)


    result = 0               
    for i in range(1, m+1):  
        if selected[i] >= 0:         
            result += 1   
    print(selected)
    print(result)

 

코드가 한 번에 이해가 안될 경우에는 펜 잡고 예시 그래도 천천히 따라가다 보면 어느 순간 이해하실 겁니다.

이분매칭 알고리즘 활용해서 아래 문제 한 번 풀어보시죠!

https://www.acmicpc.net/problem/2188

2188번: 축사 배정